堆的实现

博主： spirit
发布时间：2020 年 12 月 18 日
1332 次浏览
暂无评论
1275字数
分类：基础数据结构

[数据结构和算法动态可视化](https://visualgo.net/zh)

## 一、什么是堆？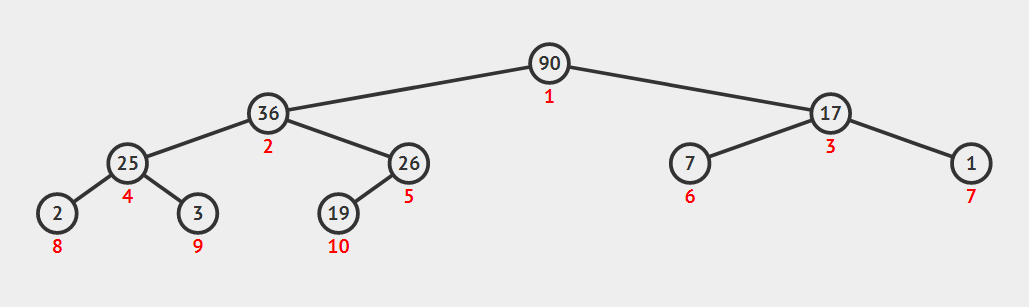

![最大堆示例](https://i.loli.net/2020/12/18/SFBt7W1wxyNcTqi.png)

（图中序列：2,7,26,25,19,17,1,90,3,36）

图中为一个最大堆，本篇博客以最大堆为例实现一个堆。

- 堆的结构：堆是一棵完全二叉树。
- 堆的有序性：对于堆中的任意一个节点，其父节点的值一定大于等于当前节点，子节点的值一定小于等于当前节点。

由这两条性质显然可以得出结论，堆顶（二叉树树根）元素的值一定是堆中元素的最大值。堆的操作的核心就是维护这两条性质。

## 二、元素的插入

1. 假设当前堆的大小为 $n$，将要插入的元素放到节点 $n + 1$ 位置处。这个操作是为了维护堆的结构。
2. 假设当前节点为 $p$，若该元素值大于其父节点的值，将节点 $p$ 与其父节点的值交换，并将 $p$ 更新为 $p/2$（即 $p$ 的父节点ID）。
3. 重复进行操作 $2$ 直至节点 $p$ 的值小于等于其父节点的值或者p到达堆顶。操作 $2$ 和操作 $3$ 维护了堆的有序性。

当一个新的元素被放在堆的最后一层时，显然除了该元素的位置与其父节点外的其他位置都是满足堆的有序性的。若新节点和它的父节点不满足堆的性质，就需要交换两个节点的元素。完成这个操作后，新节点与其父节点之间已经满足堆的性质，但由于它的父节点的值发生了变化，它的父节点与父节点的父节点之间可能不再满足有序性，因此需要循环操作直至到达堆顶或者无需上述操作即可维护堆的有序性时跳出循环。

```cpp
void up(int p) {
    while (p / 2 >= 0 && heap[p / 2] < heap[p]) {
        swap(heap[p / 2], heap[p]);
        p /= 2;
    }
}
void Insert(int x) {
    heap[++n] = x;
    up(n);
}
```

## 三、元素的删除

*注意这里的元素特指堆顶元素。

1. 用最后一个节点（即节点 $n$ ）的值覆盖掉堆顶元素，然后令堆的大小减 $1$ ，即可维护堆的结构。
2. 假设当前节点为 $p$ ，其子节点ID为 $2 · p$ 和 $2 · p + 1$。与插入元素类似，此时只有节点 $p$ 与其子节点可能破坏了有序性，将 $p$ 与子节点中的较大值比较，若节点 $p$ 的值小，就把两个节点元素交换，同时把 $p$ 更新为对应子节点ID。
3. 重复进行操作 $2$ 直至 $p$ 到达叶子节点或者节点 $p$ 的值大于它子节点的值。

```cpp
void down(int p) {
    int c;
    while (2 * p <= n) {
        c = p * 2;
        if (c + 1 <= n && heap[c + 1] > heap[c]) c += 1;
        if (heap[p] < heap[c]) {
            swap(heap[p], heap[c]);
            p = c;
        } else {
            break;
        }
    }
}
void Delete() {
    swap(heap[1], heap[n --]);
    down(1);
}
```

## 四、建堆

- 一种朴素的建堆方式就是对于每一个元素依次插入到堆中即可。
- **在数组上原地建堆**：对于给定的一个数组，按照完全二叉树的结构来看，编号最大且有子节点的节点为 $n/2$ 。从该节点开始到根节点进行循环，每次对当前节点进行向下调整操作即可。容易看出对于任意节点 $p$ 进行 $down$ 操作的时候，以它的子节点为根的完全二叉树已经是一个调整好的堆了。同时该算法的时间复杂度可以达到 $O(n)$。

```cpp
void buildHeap() {
    for (int i = n / 2; i; i --) down(i);
}
```

## 五、*删除任意一个元素

注：操作五和操作六以删除和修改第 $k$ 个插入的元素为例。

要完成这两个操作，最重要的是记录和维护第 $k$ 个插入的元素在堆中对应的节点编号。因此我们再使用两个数组，$ph[k]$ 表示第 $k$个插入的元素在堆中对应的节点编号，$hp[k]$ 表示节点 $k$ 是第几次插入的元素。而堆的所有操作中，使元素发生位置变化的只有 $swap$ 操作，我们只需要在交换元素的同时将其对应的 $ph[k]$ 和 $hp[k]$ 也交换一下即可。

```cpp
void heap_swap(int a, int b) {
    swap(ph[hp[a]], ph[hp[b]]);
    swap(hp[a], hp[b]);
    swap(heap[a], heap[b]);
}
```

- 与删除堆顶类似，我们只需要先将第k次插入的元素和堆的最后一个元素交换位置，把堆的大小减一然后维护堆的有序性即可。不过由于我们不知道应该执行 $up$ 操作还是 $down$ 操作，所以代码中要把这两个操作都写上，实际执行时只会执行其中一个。

```cpp
void heapPop(int k) {
    k = ph[k];
    heap_swap(k, n--);
    up(k);
    down(k);
}
```

## 六、*修改任意一个元素

- 该操作与操作五基本一致，把第 $k$ 次插入的元素所在节点的值更新一下即可，然后进行 $up$ 操作和 $down$ 操作。

```cpp
void heapChange(int x, int k) {
    k = ph[k];
    heap[k] = x;
    up(k);
    down(k);
}
```

## 七、完整代码

```cpp
#include <algorithm>
#include <cstdio>
#include <cstring>
#include <iostream>

using namespace std;
const int N = 1e5 + 10;
int heap[N], hp[N], ph[N], n, m;

void heap_swap(int a, int b) {
    swap(ph[hp[a]], ph[hp[b]]);
    swap(hp[a], hp[b]);
    swap(heap[a], heap[b]);
}

void down(int p) {
    int c;
    while (2 * p <= n) {
        c = p * 2;
        if (c + 1 <= n && heap[c + 1] > heap[c]) c += 1;
        if (heap[p] < heap[c]) {
            heap_swap(p, c);
            p = c;
        } else {
            break;
        }
    }
}
void heapPop() {
    heap_swap(1, n--);
    down(1);
}

void buildHeap() {
    for (int i = n / 2; i; i --) down(i);
}

void up(int p) {
    while (p / 2 > 0 && heap[p / 2] < heap[p]) {
        heap_swap(p / 2, p);
        p /= 2;
    }
}

void heapPush(int x, int k) {
    heap[++n] = x;
    ph[k] = n;
    hp[n] = k;
    up(n);
}

void heapPop(int k) {
    k = ph[k];
    heap_swap(k, n--);
    up(k);
    down(k);
}

void heapChange(int x, int k) {
    k = ph[k];
    heap[k] = x;
    up(k);
    down(k);
}
```

```

最后修改：2021 年 02 月 09 日

如果觉得我的文章对你有用，请随意赞赏

发表评论取消回复
使用cookie技术保留您的个人信息以便您下次快速评论，继续评论表示您已同意该条款

评论 *

私密评论

名称 *

🎲

邮箱 *

地址

堆的实现

spirit • 2020 年 12 月 18 日