Kattis Fruit Slicer （计算几何 + 扫描线）

博主： spirit
发布时间：2021 年 06 月 17 日
3304 次浏览
暂无评论
1635字数
分类： VJ训练赛计算几何

# Kattis Fruit Slicer （计算几何 + 扫描线）

> 参考链接
> 
> [HDU 4116 Fruit Ninja （ 计算几何 + 扫描线 ）](https://blog.csdn.net/Ezereal/article/details/52667744)

## 题意

给 $n$ 个圆的圆心坐标和半径（ $1 \leq n \leq 100)$ ，求用一条直线最多能与几个圆相交（相切也算）。

**Input1**

```
5
1.00 5.00
3.00 3.00
4.00 2.00
6.00 4.50
7.00 1.00
```

**Output1**

```
4
```

**Input2**

```
3
-1.50 -1.00
1.50 -1.00
0.00 1.00
```

**Output2**

```
3
```

## 思路

临界条件一定是至少两个圆的公切线，因为任何一个最优解都可以通过平移旋转的方式调整为两个圆的公切线。

最容易想到的做法是枚举两个圆的公切线然后暴力判断，但是有点难写，而且 $O(n^3)$ 的时间复杂度太高。

考虑枚举每个圆作为“中心圆“，模拟它的切线按照逆时针或顺时针的顺序移动的情况。某些时刻切线可以碰到一个新的圆，在一段时间后会离开这个圆。显然这些临界线都是圆的切线，我们求出中心圆与其他圆的切线，按照角度排好序之后遍历模拟切线转动过程即可。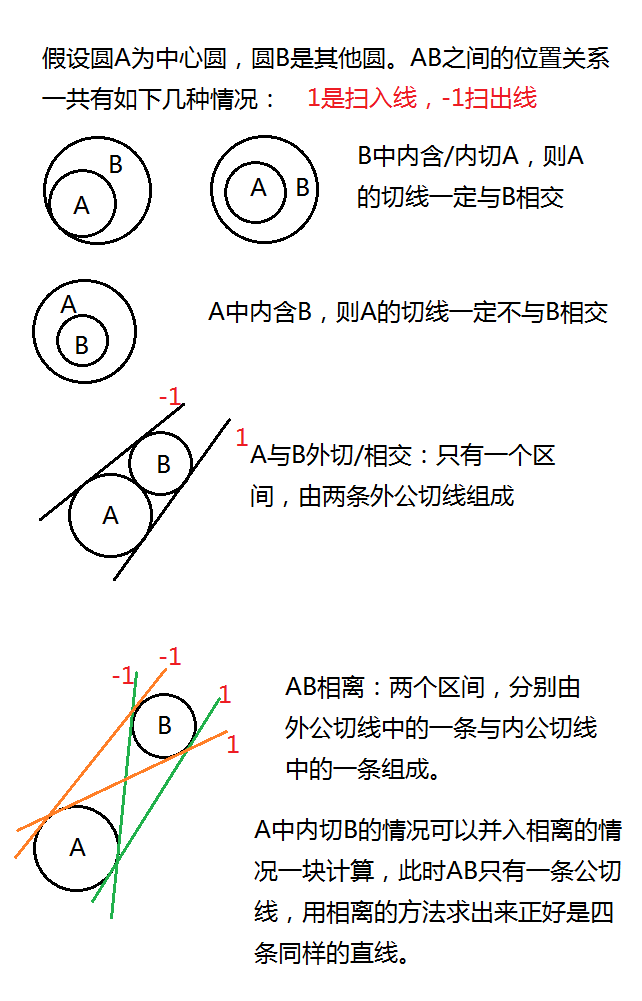

![两圆相对位置的不同情况](https://ossimage.rclouds.top/img/Kattis-Fruit-Slicer-20210617201228.png)

稍微解释一下为什么外切的情况可以视为相交的情况，考虑一下模拟切线转动的情况，外切的那条切线一定在另外两条切线的转动区间之内，所以无需考虑这条线。

## 代码

```cpp
#include <bits/stdc++.h>
#define x first
#define y second
using namespace std;
const int N = 105;
//eps太大有可能精度不够
const double eps = 1e-10, PI = acos(-1.0);
typedef pair<double, double> PDD;
struct Line {
    int id;
    double k;
    int mark;
}L[N << 4];
struct Circle {
    PDD o;
    double r;
}C[N];
int t, n, cnt;
bool vis[N];
int sign(double x) {
    if (fabs(x) < eps) return 0;
    if (x < 0) return -1;
    return 1;
}
int dcmp(double x, double y) {
    if (fabs(x - y) < eps) return 0;
    if (x < y) return -1;
    return 1;
}
bool cmp(Line &a, Line &b) {
    int tmp = dcmp(a.k, b.k);
    if (tmp) return tmp < 0;
    return a.mark > b.mark;
}
double get_dist(PDD a, PDD b) {
    double dx = a.x - b.x;
    double dy = a.y - b.y;
    return sqrt(dx * dx + dy * dy);
}
//将角度统一为[0,360]之间的角
double std_angle(double ang) {
    if (sign(ang) < 0) ang += 2 * PI;
    if (dcmp(ang, 2 * PI) > 0) ang -= 2 * PI;
    return ang;
}
void get_k(Circle a, Circle b, int id, int &sum) {
    double base = atan2(b.o.y - a.o.y, b.o.x - a.o.x);
    double dis = get_dist(a.o, b.o);
    //A内含B
    if (dcmp(dis + b.r, a.r) < 0) return ;
    //B内含/内切A
    if (dcmp(dis + a.r, b.r) <= 0) {
        sum++;
        return ;
    }
    double ang1 = asin((b.r - a.r) / dis);
    double ang2 = asin((b.r + a.r) / dis);
    //A、B相交/外切
    if (dcmp(dis, a.r + b.r) <= 0) {
        L[cnt++] = {id, std_angle(base - ang1), 1};
        L[cnt++] = {id, std_angle(base + ang1 + PI), -1};
        return ;
    }
    //A、B相离
    L[cnt++] = {id, std_angle(base - ang1), 1};
    L[cnt++] = {id, std_angle(base + ang2), -1};
    L[cnt++] = {id, std_angle(base - ang2 + PI), 1};
    L[cnt++] = {id, std_angle(base + ang1 + PI), -1};
    //注意上面几行的角度处理，从一条线转到另一条线的实际角度是多少
}
int get(int id) {
    cnt = 0;
    int res, sum = 1;
    for (int i = 1; i <= n; i++) 
        if (i != id) get_k(C[i], C[id], i, sum);
    sort(L, L + cnt, cmp);
    memset(vis, false, sizeof vis);
    //因为不知道从哪里开始最优所以枚举两圈
    int m = cnt << 1;
    res = sum;
    for (int i = 0; i < m; i++) {
        int k = i % cnt;
        if (L[k].mark == 1) {
            if (!vis[L[k].id]) {
                vis[L[k].id] = true;
                sum++;
            }
        } else {
            if (vis[L[k].id]) {
                vis[L[k].id] = false;
                sum--;
            }
        }
        if (sum > res) res = sum;
    }
    return res;
}
int main() {
    scanf("%d", &n);
    for (int i = 1; i <= n; i++) {
        scanf("%lf %lf", &C[i].o.x, &C[i].o.y);
        C[i].r = 1;
    }
    int res = 0;
    for (int i = 1; i <= n; i++) 
        res = max(res, get(i));
    printf("%d\n", res);
    return 0;
}
```

最后修改：2021 年 06 月 17 日

如果觉得我的文章对你有用，请随意赞赏

发表评论取消回复
使用cookie技术保留您的个人信息以便您下次快速评论，继续评论表示您已同意该条款

评论 *

私密评论

名称 *

🎲

邮箱 *

地址

Kattis Fruit Slicer （计算几何 + 扫描线）

spirit • 2021 年 06 月 17 日

# Kattis Fruit Slicer （计算几何 + 扫描线）

> 参考链接
> 
> [HDU 4116 Fruit Ninja （ 计算几何 + 扫描线 ）](https://blog.csdn.net/Ezereal/article/details/52667744)

## 题意

给 $n$ 个圆的圆心坐标和半径（ $1 \leq n \leq 100)$ ，求用一条直线最多能与几个圆相交（相切也算）。

**Input1**

```
5
1.00 5.00
3.00 3.00
4.00 2.00
6.00 4.50
7.00 1.00
```

**Output1**

```
4
```

**Input2**

```
3
-1.50 -1.00
1.50 -1.00
0.00 1.00
```

**Output2**

```
3
```

## 思路

临界条件一定是至少两个圆的公切线，因为任何一个最优解都可以通过平移旋转的方式调整为两个圆的公切线。

最容易想到的做法是枚举两个圆的公切线然后暴力判断，但是有点难写，而且 $O(n^3)$ 的时间复杂度太高。

![两圆相对位置的不同情况](https://ossimage.rclouds.top/img/Kattis-Fruit-Slicer-20210617201228.png)

## 代码

Kattis Fruit Slicer （计算几何 + 扫描线）

发表评论取消回复
使用cookie技术保留您的个人信息以便您下次快速评论，继续评论表示您已同意该条款

Kattis Message （状态机模型 + 矩阵快速幂）

数论进阶——莫比乌斯反演

Codeforces Round #703 (Div. 2)

SDUT 2021 Winter Individual Contest - E

Kattis Fruit Slicer （计算几何 + 扫描线）

2020 ICPC EC-Final A题

L3-030 可怜的简单题（2021天梯赛 L3-3）

SDUT 2021 Winter Individual Contest - G

Codeforces Round #703 (Div. 2)

SDUT 2021 Winter Individual Contest - E

Kattis Fruit Slicer （计算几何 + 扫描线）

发表评论 取消回复 使用cookie技术保留您的个人信息以便您下次快速评论，继续评论表示您已同意该条款

Kattis Fruit Slicer （计算几何 + 扫描线）

发表评论取消回复
使用cookie技术保留您的个人信息以便您下次快速评论，继续评论表示您已同意该条款