计算几何基础知识

博主： spirit
发布时间：2021 年 02 月 20 日
1674 次浏览
暂无评论
3698字数
分类：计算几何

# 计算几何基础知识

## 一、前置知识点

1. $\pi = acos(-1.0)$
2. 余弦定理：$c^2 = a^2 + b^2 - 2abcos\theta$
   
   正弦定理：$\frac{a}{sin\alpha} = \frac{b}{sin\beta} = \frac{c}{sin\theta}$

## 二、浮点数比较

```cpp
const double eps = 1e-8;
int sign(double x) {//符号函数
    if (fabs(x) < eps) return 0;
    if (x < 0) return -1;
    return 1;
}
int cmp(double x, double y) {//比较函数
    if (fabs(x - y) < eps) return 0;
    if (x < y) return -1;
    return 0;
}
```

## 三、向量

### 向量的加减法与数乘运算

1. 加法：$\vec A(x1, y1) + \vec B(x2, y2) = \vec C(x1 + x2, y1 + y2)$
2. 减法：$\vec A(x1, y1) - \vec B(x2, y2) = \vec C(x1 - x2, y1 - y2)$
3. 数乘：$a \cdot \vec A(x1, y1) = (a \cdot x1, a \cdot y1)$

### 内积（点积）

$\vec A \cdot \vec B = |\vec A| \ |\vec B| \ cos\theta$

1. 几何意义：$\vec A$ 在 $\vec B$ 上的投影与 $|\vec B|$ 的乘积。
2. 代码实现：
   
   ```cpp
   double dot(Point a, Point b) {
       return a.x * b.x + a.y * b.y;
   }
   ```

### 外积（叉积）

$\vec A \times \vec B = |\vec A| \ |\vec B| \ sin\theta$

1. 几何意义：$\vec A$ 与 $\vec B$ 张成的平行四边形的有向面积。$\vec B$ 在 $\vec A$ 的逆时针方向为正。
2. 代码实现：
   
   ```cpp
   double corss(Point a, Point b) {
       return a.x * b.y - b.x * a.y;
   }
   ```

### 常用函数

1. 取模
   
   ```cpp
   double get_length(Point a) {
       return sqrt(dot(a, a));
   }
   ```
2. 计算向量夹角
   
   ```cpp
   double get_angle(Point a, Point b) {
       return acos(dot(a, b) / get_length(a) / get_length(b));
   }
   ```
3. 计算两个向量构成的平行四边形有向面积
   
   ```cpp
   double area(Point a, Point b, Point c) {
       return cross(b - a, c - a);
   }
   ```
4. $\vec A$ 顺时针旋转 $C$ 角度后的坐标
   
   ```cpp
   Point rotate(Point a, double angle) {
       return Point(a.x * cos(angle) + a.y * sin(angle), -a.x * sin(angle) + a.y * cos(angle));
   }
   ```

## 四、点与线

### 直线表达式

1. 一般式：$ax + by + c = 0$
2. 点向式：$p_0 + t \cdot \vec v$ （最常用，下文基本都是点向式）
3. 斜截式：$y = kx + b$

### 常用操作

1. 判断点在直线上：$\vec A \times \vec B = 0$ ，即 $\vec v$ 与 $p - p_0$
2. 两直线交点：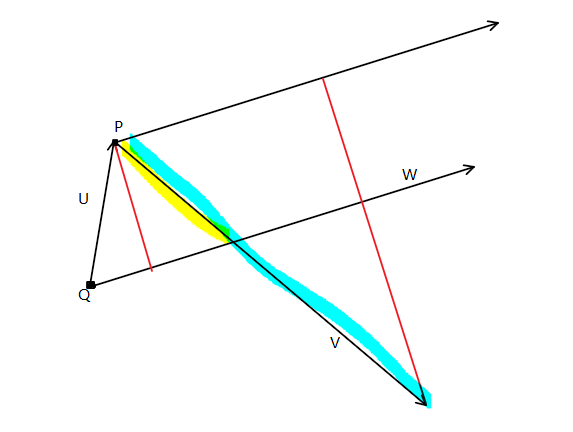
   
   ![](https://i.loli.net/2021/02/20/ryZVojne6p9XMSR.png)
   如上图所示，已知向量的叉积表示平行四边形的面积，同时平行四边形在底边相同的情况下，面积之比等于高之比，可知 $\frac{\vec w \times \vec u}{\vec v \times \vec w}$ 就是高的比值（即图中两条红线）。由相似三角形可知，高的比值即为图中黄色部分线段与蓝色部分线段之比，这样就得到了系数 $t$ ，由点向式可直接得出交点。
   
   ```cpp
   Point get_line_intersection(Point p, Vector v, Point q, Vector w) {
       Vector u = p - q;
       double t = cross(w, u) / cross(v, w);
       return p + t * v;
   }
   ```
3. 点到直线的距离：由叉积的定义可以推导
   
   ```cpp
   double distance_to_line(Point p, Point a, Point b) {
       Vector v1 = b - a, v2 = p - a;
       return fabs(cross(v1, v2) / get_length(v1));
   }
   ```
4. 点到线段的距离：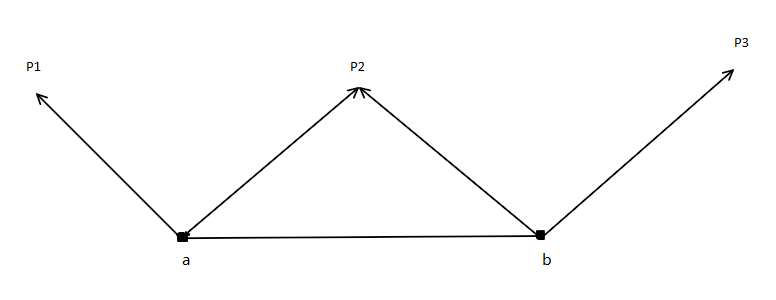
   
   ![](https://i.loli.net/2021/02/20/KaRtw7NklUZ4exE.png)
   
   记$\vec v_1 = b - a \quad \vec v_2 = p - a \quad \vec v_3 = p - b$ ，若点 $p$ 在 $p_1$ 位置，可以发现 $\vec v_1 \cdot \vec v_2 < 0$ ，此时距离即为 $|\vec v_2|$ ；若点 $p$ 在 $p_3$ 位置，则 $\vec v_1 \cdot \vec v_3 > 0$ ，此时距离即为 $|\vec v_3|$；否则点 $p$ 位于 $p_2$ 位置，此时距离为点 $p$ 至直线 $ab$ 的距离。
   
   ```cpp
   dobule distance_to_segment(Point p, Point a, Point b) {
       if (a == b) return get_length(p - a);
       Vector v1 = b - a, v2 = p - a, v3 = p - b;
       if (cdot(v1, v2) < 0) return get_length(v2);
       if (cdot(v1, v3) > 0) return get_length(v3);
       return distance_to_line(p, a, b);
   }
   ```
5. 点在直线上的投影：
   
   ```cpp
   Point get_line_projection(Point p, Point a, Point b) {
       Vector v = b - a;
       return a + dot(v, p - a) / dot(v, v) * v;
   }
   ```
6. 点是否在线段上：
   
   先判断点 $p$ 在直线 $a b$ 上，再判断是否在线段 $ab$ 上。
   
   ```cpp
   bool on_segment(Point p, Point a, Point b) {
       return sign(cross(p - a, p - b)) == 0 && sign(dot(p - a, p - b)) <= 0;
   }
   ```
7. 判断两线段是否相交：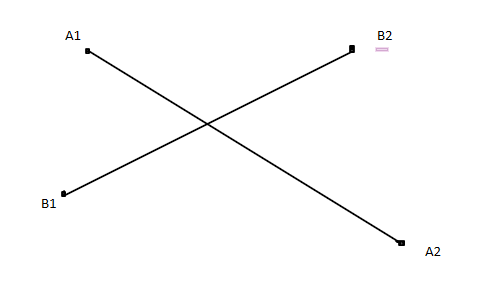
   
   ![](https://i.loli.net/2021/02/20/3F7NaHmpAuEqR9s.png)
   
   判断同时满足：$a_1 \ a_2$ 在直线 $b_1 b_2$ 的两侧，$b_1 \ b_2$ 在直线 $a_1 a_2$ 的两侧即可。
   
   ```cpp
   bool segment_intersection(Point a1, Point a2, Point b1, Point b2) {
       double c1 = cross(a2 - a1, b1 - a1), c2 = cross(a2 - a1, b2 - a1);
       double c3 = corss(b2 - b1, a1 - b1), c4 = cross(b2 - b1, a2 - b1);
       return sign(c1) * sign(c2) <= 0 && sign(c3) * sign(c4) <= 0;
   }
   ```

## 五、多边形

### 三角形

1. 面积：
   - 叉积的一半
   - 海伦公式：$p = \frac{a + b + c}{2} \quad S = \sqrt{p \cdot (p - a) \cdot (p - b) \cdot (p - c)}$
2. 三角形的四心：
   - 外心：外接圆圆心。三边中垂线交点，到三个顶点距离相等。
   - 内心：内切圆圆心，角平分线交点，到三边距离相等。
   - 垂心：三条垂线交点。
   - 重心：三条中线交点（到三角形三顶点距离的平方和最小的点，三角形内到三边距离之积最大的点）。

### 普通多边形

通常按逆时针储存所有的点

1. 定义
   
   - 多边形：由在同一平面且不再同一直线上的多条线段首尾顺次连接且不相交所组成的图形叫多边形。
   - 简单多边形：简单多边形是除相邻边外其它边不相交的多边形。
   - 凸多边形：过多边形的任意一边做一条直线，其他所有顶点都在该直线的同侧，则这个多边形是凸多边形。
     
     任意凸多边形的外角和为 $360°$
     
     任意凸多边形的内角和为 $(n - 2) \cdot 180°$
2. 常用函数
   
   - 求多边形面积面积（未必是凸多边形）
     
     从第一个顶点开始把多边形分成 $n - 2$ 个三角形，求面积和即可。
     
     ```cpp
     double polygon_area(Point p[], int n) {
         double s = 0;
         for (int i = 1; i + 1 < n; i++) 
             s += cross(p[i] - p[0], p[i + 1] - p[i]);
         return s / 2;
     }
     ```
   - 判断点是否在多边形内（不一定是凸多边形）
     
     - 射线法：从该点任意做一条和所有边都不平行的射线。与多边形交点为偶数，则在多边形外，为奇数，则在多边形内。
     - 转角法：按照逆时针顺序从该点到每条边连线，转过 $360°$ 说明在多边形内，转过 $0°$ 则在多边形外。
   - 判断点是否在凸多边形内：判断点是否在所有边的左边即可。
3. 皮克定理
   
   皮克定理是指一个计算点阵中顶点在格点上的多边形面积公式该公式可以表示为:
   
   $$
   S = a + \frac{b}{2} - 1
   $$
   
   其中 $a$ 表示多边形内部的点数，$b$ 表示多边形边界上的点数，$S$ 表示多边形的面积。

最后修改：2021 年 05 月 22 日

如果觉得我的文章对你有用，请随意赞赏

发表评论取消回复
使用cookie技术保留您的个人信息以便您下次快速评论，继续评论表示您已同意该条款

评论 *

私密评论

名称 *

🎲

邮箱 *

地址

计算几何基础知识

spirit • 2021 年 02 月 20 日

# 计算几何基础知识

## 一、前置知识点

1. $\pi = acos(-1.0)$
2. 余弦定理：$c^2 = a^2 + b^2 - 2abcos\theta$
   
   正弦定理：$\frac{a}{sin\alpha} = \frac{b}{sin\beta} = \frac{c}{sin\theta}$

## 二、浮点数比较

## 三、向量

### 向量的加减法与数乘运算

### 内积（点积）

$\vec A \cdot \vec B = |\vec A| \ |\vec B| \ cos\theta$

1. 几何意义：$\vec A$ 在 $\vec B$ 上的投影与 $|\vec B|$ 的乘积。
2. 代码实现：
   
   ```cpp
   double dot(Point a, Point b) {
       return a.x * b.x + a.y * b.y;
   }
   ```

### 外积（叉积）

$\vec A \times \vec B = |\vec A| \ |\vec B| \ sin\theta$

### 常用函数

## 四、点与线

### 直线表达式

1. 一般式：$ax + by + c = 0$
2. 点向式：$p_0 + t \cdot \vec v$ （最常用，下文基本都是点向式）
3. 斜截式：$y = kx + b$

### 常用操作

## 五、多边形

### 三角形

### 普通多边形

通常按逆时针储存所有的点

计算几何基础知识

发表评论取消回复
使用cookie技术保留您的个人信息以便您下次快速评论，继续评论表示您已同意该条款

Kattis Message （状态机模型 + 矩阵快速幂）

数论进阶——莫比乌斯反演

Codeforces Round #703 (Div. 2)

SDUT 2021 Winter Individual Contest - E

Kattis Fruit Slicer （计算几何 + 扫描线）

SDUT 2021 Winter Individual Contest - F

数论进阶——莫比乌斯反演

Kattis Terraced fields （数位DP）

堆的实现

SDUT 2021 Winter Individual Contest - E

计算几何基础知识

发表评论 取消回复 使用cookie技术保留您的个人信息以便您下次快速评论，继续评论表示您已同意该条款

计算几何基础知识

发表评论取消回复
使用cookie技术保留您的个人信息以便您下次快速评论，继续评论表示您已同意该条款